手册
- Unity 用户手册 2020.3 (LTS)
- New in Unity 2020 LTS
- 包
- 已验证包
- 2D Animation
- 2D Pixel Perfect
- 2D PSD Importer
- 2D SpriteShape
- Adaptive Performance
- Addressables
- Advertisement
- Alembic
- Analytics Library
- Android Logcat
- Animation Rigging
- AR Foundation
- ARCore XR Plugin
- ARKit Face Tracking
- ARKit XR Plugin
- Burst
- Cinemachine
- Code Coverage
- Core RP Library
- Editor Coroutines
- FBX Exporter
- High Definition RP
- In App Purchasing
- Input System
- iOS 14 广告支持
- JetBrains Rider 编辑器
- Magic Leap XR Plugin
- ML Agents
- Mobile Notifications
- Multiplayer HLAPI
- Oculus XR Plugin
- OpenXR 插件
- Polybrush
- Post Processing
- ProBuilder
- Profile Analyzer
- Quick Search
- Recorder
- Remote Config
- Scriptable Build Pipeline
- Shader Graph
- Test Framework
- TextMeshPro
- 时间轴
- Unity Distribution Portal
- Universal RP
- 版本控制
- Visual Effect Graph
- Visual Studio Code 编辑器
- Visual Studio 编辑器
- WebGL Publisher
- Windows XR Plugin
- Xiaomi SDK
- XR Plugin Management
- 预览包
- 核心包
- 内置包
- AI
- Android JNI
- 动画
- Asset Bundle
- Audio
- 布料
- Director
- Image Conversion
- IMGUI
- JSONSerialize
- Particle System
- 物理 (Physics)
- Physics 2D
- Screen Capture
- Terrain
- Terrain Physics
- Tilemap
- UI
- UIElements
- Umbra
- Unity Analytics
- Unity Web Request
- Unity Web Request Asset Bundle
- Unity Web Request Audio
- Unity Web Request Texture
- Unity Web Request WWW
- Vehicles
- Video
- VR
- Wind
- XR
- 按关键字排列的包
- Unity 的 Package Manager
- 创建自定义包
- 已验证包
- 在 Unity 中操作
- 安装 Unity
- 升级 Unity
- Unity 的界面
- 创建游戏玩法
- 编辑器功能
- 分析
- Asset Workflow
- 输入
- 2D
- 图形
- 渲染管线
- 摄像机
- 后期处理
- 光照
- 支持的模型文件格式
- 网格
- 纹理
- 着色器
- Shaders core concepts
- 内置着色器
- 标准着色器
- 标准粒子着色器
- Autodesk Interactive 着色器
- 旧版着色器
- 内置着色器的用途和性能
- 普通着色器系列
- 透明着色器系列
- 透明镂空着色器系列
- 自发光着色器系列
- 反光着色器系列
- 反射顶点光照 (Reflective Vertex-Lit)
- 反光漫射 (Reflective Diffuse)
- 反光镜面反射 (Reflective Specular)
- 反光凹凸漫射 (Reflective Bumped Diffuse)
- 反光凹凸镜面反射 (Reflective Bumped Specular)
- 反光视差漫射 (Reflective Parallax Diffuse)
- 反光视差镜面反射 (Reflective Parallax Specular)
- 反光法线贴图无光照 (Reflective Normal Mapped Unlit)
- 反光法线贴图顶点光照 (Reflective Normal mapped Vertex-lit)
- 使用 Shader Graph
- 编写着色器
- 编写着色器概述
- ShaderLab
- ShaderLab:定义 Shader 对象
- ShaderLab:定义子着色器
- ShaderLab:定义一个通道
- ShaderLab:添加着色器程序
- ShaderLab:命令
- ShaderLab:使用 Category 代码块对命令进行分组
- ShaderLab 命令:AlphaToMask
- ShaderLab 命令:Blend
- ShaderLab 命令:BlendOp
- ShaderLab 命令:ColorMask
- ShaderLab 命令:Conservative
- ShaderLab 命令:Cull
- ShaderLab 命令:Offset
- ShaderLab 命令:模板
- ShaderLab 命令:UsePass
- ShaderLab 命令:GrabPass
- ShaderLab 命令:ZClip
- ShaderLab 命令:ZTest
- ShaderLab 命令:ZWrite
- ShaderLab 旧版功能
- Unity 中的 HLSL
- Unity 中的 GLSL
- Example shaders
- 编写表面着色器
- 为不同的图形 API 编写着色器
- 着色器性能和性能分析
- 材质
- 粒子系统
- 选择粒子系统解决方案
- 内置粒子系统
- 使用内置粒子系统
- 粒子系统顶点流和标准着色器支持
- 粒子系统 GPU 实例化
- 粒子系统 C# 作业系统集成
- 组件和模块
- 粒子系统 (Particle System)
- 粒子系统模块
- 粒子系统 (Particle System) 主模块
- Emission 模块
- Shape 模块
- Velocity over Lifetime 模块
- Noise 模块
- Limit Velocity Over Lifetime 模块
- Inherit Velocity 模块
- Lifetime by Emitter Speed
- Force Over Lifetime 模块
- Color Over Lifetime 模块
- Color By Speed 模块
- Size over Lifetime 模块
- Size by Speed 模块
- Rotation Over Lifetime 模块
- Rotation By Speed 模块
- External Forces 模块
- Collision 模块
- Triggers 模块
- Sub Emitters 模块
- Texture Sheet Animation 模块
- Lights 模块
- Trails 模块
- Custom Data 模块
- Renderer 模块
- 粒子系统力场 (Particle System Force Field)
- 内置粒子系统示例
- Visual Effect Graph
- 创建环境
- 天空
- 视觉效果组件
- 高级渲染功能
- 优化图形性能
- Color
- 物理系统
- 脚本
- 多玩家和联网
- 音频
- 视频概述
- 动画
- 创建用户界面 (UI)
- 导航和寻路
- Unity 服务
- Setting up your project for Unity services
- Unity Organizations
- Unity Ads
- Unity Analytics
- Unity Cloud Build
- Automated Build Generation
- 支持的平台
- 支持的 Unity 版本
- 共享链接
- 版本控制系统
- 使用 Unity 开发者控制面板 (Developer Dashboard) 对 Unity Cloud Build 进行 Git 配置
- 使用 Unity 开发者控制面板 (Developer Dashboard) 对 Unity Cloud Build 进行 Mercurial 配置
- 将 Apache Subversion (SVN) 用于 Unity Cloud Build
- 使用 Unity 开发者控制面板 (Developer Dashboard) 对 Unity Cloud Build 进行 Perforce 配置
- 使用 Unity 开发者控制面板 (Developer Dashboard) 对 Unity Cloud Build 进行 Plastic 配置
- 发布到 iOS
- 高级选项
- 在 Unity Cloud Build 中使用可寻址资源
- 编译清单
- 计划构建
- Cloud Build REST API
- Unity Cloud Content Delivery
- Unity IAP
- Setting up Unity IAP
- 跨平台指南
- 应用商店指南
- 实现应用商店
- Unity Collaborate
- Setting up Unity Collaborate
- Adding team members to your Unity project
- 查看历史记录
- Enabling Cloud Build with Collaborate
- 管理 Unity Editor 版本
- Reverting files
- Resolving file conflicts
- 排除资源使其不发布到 Collaborate
- 将单个文件发布到 Collaborate
- 还原项目至以前的版本
- 进行中 (In-Progress) 编辑通知
- 管理云存储
- 将项目移动到另一个版本控制系统
- Unity Accelerator
- Collaborate troubleshooting tips
- Unity Cloud Diagnostics
- Unity Integrations
- Multiplayer 服务
- Unity 分发平台
- XR
- 开源代码仓库
- Unity Asset Store
- 平台开发
- 将“Unity 用作库”用于其他应用程序
- 启用深层链接
- 独立平台
- macOS
- Apple TV
- WebGL
- iOS
- Android
- Windows
- 将 Unity 集成到 Windows 和 UWP 应用程序中
- Windows 通用
- 通用 Windows 平台
- 已知问题
- 旧版主题
- 术语表
- Unity 用户手册 2020.3 (LTS)
- 脚本
- 重要的类
- 重要的类 - Random
重要的类 - Random
Random 类为您提供了简便的方法,可生成各种常用类型的随机值。
此页面概述了 Random 类及其使用该类编写脚本时的常见用法。有关 Random 类的每个成员的详尽参考以及有关它的更多技术细节,请参阅 Random 脚本参考。
请点击以下链接,了解这些有用方法的更多详细信息和示例。
简单的随机数
Random.value 返回一个随机浮点数,范围在 0.0 和 1.0 之间。一种常见的用法是将返回结果乘以所选范围,从而将其转换为介于 0 和该范围之间的数。
Random.Range 返回一个介于所提供的最小值和最大值之间的数。它返回整数或浮点数,具体取决于提供的最小值和最大值是整数还是浮点数。
圆形或球体内的随机点
Random.insideUnitCircle 返回一个半径为 1 的圆内随机选择的圆内点(同样,您可以将结果相乘,获得任意大小的圆内的随机点)。
Random.insideUnitSphere 返回一个半径为 1 的球内随机选择的球内点。
Random.onUnitSphere 返回一个半径为 1 的球上随机选择的球体的_球面_点。
其他类型的随机值
Unity 的 Random 类还提供了一些其他类型的随机值。
要生成一个随机旋转,使用 Random-rotation。
要生成一个随机颜色,使用 Random.ColorHSV。
从数组中选择一个随机项
随机选取一个数组元素归结为选择零和数组最大索引值(等于数组的长度减去 1)之间的一个随机整数。使用内置的 Random.Range 函数可以轻松实现:
`var element = myArray[Random.Range(0, myArray.Length)];``
请注意,Random.Range 从包含第一个参数但不包含第二个参数的范围内返回一个值,因此在此处使用 myArray.Length 会得到正确的结果。
选择具有不同概率的项
有时需要随机选择项,但有些项比其他项被选中的几率更高。例如,NPC 在遇到玩家时可能会以几种不同的方式做出反应:
- 友好问候的几率为 50%
- 逃跑的几率为 25%
- 立即攻击的几率为 20%
- 提供金钱作为礼物的几率为 5%
可将这些不同的结果可视化为一张纸条,该纸条分成几个部分,每个部分占据纸条总长度的一个比例。占据的比例等于选择结果的概率。选择行为相当于沿着纸条的长度选择一个随机点(例如通过投掷飞镖),然后查看该点处于哪个部分。

在脚本中,纸条实际上是一个浮点数组,其中的浮点数按顺序包含项的不同概率。随机点是通过将 Random.value 乘以数组中所有浮点数的总和得到的(这些数值不需要加起来等于 1;重点是不同值的相对大小)。要找到该点“位于”哪个数组元素,首先要检查它是否小于第一个元素中的值。如果是,则第一个元素便是选中的元素。否则,从该点值中减去第一个元素的值,然后将其与第二个元素进行比较,依此类推,直到找到正确的元素。在代码中表示为以下所示的内容:
float Choose (float[] probs) {
float total = 0;
foreach (float elem in probs) {
total += elem;
}
float randomPoint = Random.value * total;
for (int i= 0; i < probs.Length; i++) {
if (randomPoint < probs[i]) {
return i;
}
else {
randomPoint -= probs[i];
}
}
return probs.Length - 1;
}
请注意,最后的 return 语句是必要的,因为 Random.value 可以返回 1 的结果。在这种情况下,搜索将无法在任何地方找到随机点。将以下行
`if (randomPoint < probs[i])`
…更改为“小于或等于”测试将避免额外的 return 语句,但也会允许偶尔选择某个项,即使其概率为零也是如此。
加权连续随机值
如果结果是不连续的,那么浮点数组方法会很有效,但在某些情况下希望产生更连续的结果;比如说,希望随机化一个宝箱中发现的金块数量,并希望能够出现 1 到 100 之间的任何数字,但让更小数字的概率更高。使用浮点数组方法来执行此算法将需要设置一个包含 100 个浮点数(即纸条上的部分)的数组,这是很不实用的方法;如果不局限于整数而是想要在该范围内的任何数字,则不可能使用这种方法。
一种适用于连续结果的更好方法是使用 AnimationCurve 将“原始”随机值转换为“加权”值;通过绘制不同的曲线形状,可产生不同的权重。代码编写起来也更简单:
float CurveWeightedRandom(AnimationCurve curve) {
return curve.Evaluate(Random.value);
}
此算法从 Random.value 读取值来选择 0 到 1 之间的“原始”随机值。然后,该值传递给 curve.Evaluate(),在此处将其视为水平坐标,并返回曲线在该水平位置处的相应垂直坐标。曲线较平缓的部分被选取的几率较高,而较陡峭的部分被选取的几率较低。
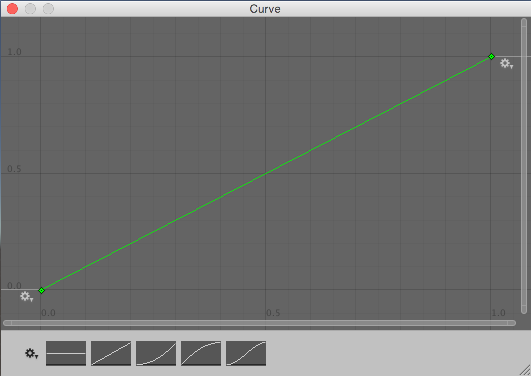
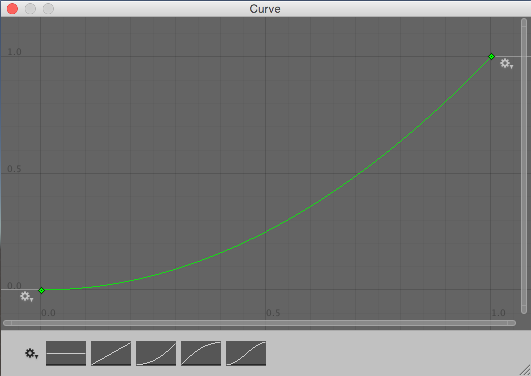
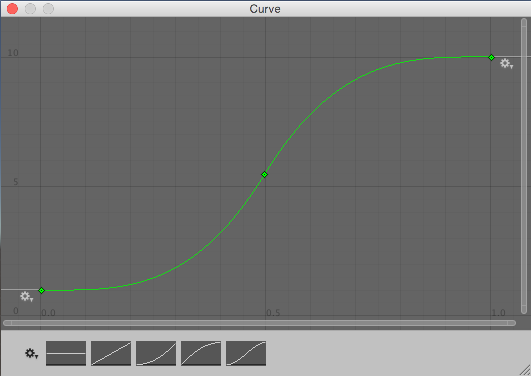
请注意,这些曲线并非概率论指南中可能介绍的概率分布曲线,而更像是反向累积概率曲线。
通过在一个脚本上定义 AnimationCurve 公共变量,可使用 Inspector 窗口直观查看和编辑曲线,而无需计算值。
这种方法会产生浮点数。如果要计算整数结果(例如,需要 82 个金块,而不是 82.1214 个金块),可将计算值传递给 Mathf.RoundToInt() 之类的函数。
列表洗牌
一种常见的游戏机制是从一组已知的项中进行选择,但让这些项以随机顺序到达。例如,一副纸牌通常需要洗牌,因此不会以可预测的顺序绘制。为了对数组中的项进行随机洗牌,可访问每个元素,然后将其与数组中位于随机索引处的另一个元素进行交换:
void Shuffle (int[] deck) {
for (int i = 0; i < deck.Length; i++) {
int temp = deck[i];
int randomIndex = Random.Range(0, deck.Length);
deck[i] = deck[randomIndex];
deck[randomIndex] = temp;
}
}
从一组无重复的项中选择
一种常见的任务是从一组中随机选取一些项,但不可多次选取同一项。例如,可能希望在一些随机生成点生成多个 NPC,但要确保每个点只生成一个 NPC。为实现此目的,可按顺序遍历这些项,随机决定是否将每一项添加到所选集合中。当访问每一项时,该项被选取的概率等于仍然需要的项数除以仍然可供选择的项数。
例如,假设有 10 个可用的生成点,但只能选择其中 5 个。选择第一项的概率为 5/10,即 0.5。如果选择了该项,那么第二项的概率将是 4/9,即 0.44(即仍然需要 4 项,还剩下 9 项可供选择)。但是,如果未选择第一项,那么第二项的概率将是 5/9,即 0.56(即仍然需要 5 项,还剩下 9 项可供选择)。这一直持续到该集合包含所需的 5 项为止。可使用如下所示的代码实现此算法:
Transform[] spawnPoints;
Transform[] ChooseSet (int numRequired) {
Transform[] result = new Transform[numRequired];
int numToChoose = numRequired;
for (int numLeft = spawnPoints.Length; numLeft > 0; numLeft--) {
float prob = (float)numToChoose/(float)numLeft;
if (Random.value <= prob) {
numToChoose--;
result[numToChoose] = spawnPoints[numLeft - 1];
if (numToChoose == 0) {
break;
}
}
}
return result;
}
请注意,虽然选择是随机的,但所选集合中的项与原始数组中的项具有相同的顺序。如果要按顺序一次使用一项,那么这种排序可能使它们在一定程度上可预测,因此在使用之前可能需要对数组进行洗牌。
空间中的随机点
通过将 Vector3 的每个分量设置为 Random.value 返回的值可以选择立方体中的随机点:
` var randVec = Vector3(Random.value, Random.value, Random.value);`
这种算法可在边长为一个单位的立方体内部给出一个点。只需将矢量的 X、Y 和 Z 分量乘以期望的边长即可缩放该立方体。如果其中一个轴设置为零,则该点将始终位于单个平面内。例如,在“地面”上选取随机点通常需要随机设置 X 和 Z 分量并将 Y 分量设置为零。
当体积为球体时(即,希望从原点开始的给定半径内选取随机点时),可使用 Random.insideUnitSphere 乘以所需的半径:
` var randWithinRadius = Random.insideUnitSphere * radius;`
请注意,如果将结果矢量的某个分量设置为零,则不能在圆内获得正确的随机点。尽管该点确实是随机点并且位于正确的半径内,但是概率严重偏向于圆的边缘,因此点分布将非常不均匀。对于此任务,应改用 Random.insideUnitCircle:
`var randWithinCircle = Random.insideUnitCircle * radius;`